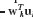MOBILITY ENGINEERING Produced by SAE Media Group
MOBILITY ENGINEERING
Magazines
Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Adaptive Deblurring of Noisy Images

A deblurring filter is designed adaptively to reduce adverse effects of noise.

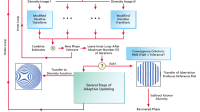
An algorithm for adaptive deblurring of images has been designed to be less adversely affected by image noise than are prior deblurring algorithms. The need for this or another noise-tolerant deblurring algorithm arises as follows: For a typical imaging instrument, in which the blurring function (also known as the point-spread function) approximates a Gaussian function in the spatial-frequency domain, a simplistic spatial-frequency-domain deblurring function equal to the inverse of the blurring function magnifies the noise at high spatial frequencies. In the present adaptive deblurring algorithm, the spatial-frequency-domain deblurring function is the product of (1) the inverse of spatial-frequency-domain blurring function and (2) a smoothing or low-pass filter function denoted variously as a power window or a P-deblurring filter function (wherein "P" signifies "power"). The term "adaptive" in the name of the algorithm characterizes the process for choosing the parameters of the power window.

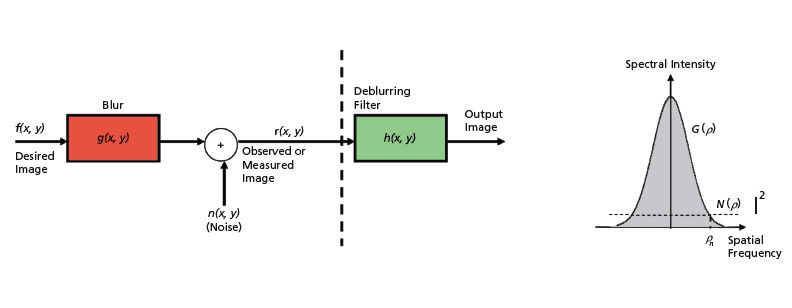
Figure 1. This Block Diagram and the spatial-frequency spectral plots represent selected aspects of the image-acquisition process (including blurring and addition of noise) and the deblurring process.
Figure 1 schematically depicts the image-acquisition and deblurring processes as modelled by the following equations. The observed or measured blurred image r(x,y) is given by

r(x,y)=f(x,y)⊗g(x,y)+n(x,y)

where x and y are Cartesian position coordinates in the image plane, f(x,y) is the non-blurred input image that one seeks to recover, g(x,y) is the blurring function in position space, ⊗ is the convolution operator, and n(x,y) is the additive image noise. In the spatial-frequency domain, the observed image is given by

R(kx,ky)=F(kx,ky)G(kx,ky)+N(kx,ky)

where kx and ky are spatial frequencies corresponding to the Cartesian coordinates and R(kx,ky), F(kx,ky), G(kx,ky), and N(kx,ky) are the Fourier transforms of r(x,y), f(x,y), g(x,y), and n(x,y), respectively. For the purpose of the algorithm, it is assumed that, as in most practical imaging systems, the blurring and noise functions are radially symmetric, so that their Fourier transforms can be expressed as G(ρ) and N(ρ), respectively, where ρ≡(kx2 + ky2)(1⁄2). It is further assumed that, as in most practical imaging systems, the noise is white in that its power spectral density, ⏐N(ρ)⏐2 can be considered approximately constant over the entire spatial-frequency range of interest.

In the deblurring process, one applies a deblurring filter denoted as h(x,y) in the position- coordinate domain or H(ρ) in the spatial-frequency domain. The problem is to choose H(ρ) to make the resulting image approximate f(x,y) with acceptably high accuracy. In the present algorithm, the deblurring filter is given by

H(ρ)=W(ρ)/G(ρ)

Figure 2. The P-Deblurring Function is the product of (1) the inverse of a Gaussian blurring function and (2) a power window described in the text. In the absence of the power window, the inverse Gaussian would cause magnification of noise at high spatial frequencies.
where W is the P-deblurring function, which is defined by the equation

W(ρ)≡exp(−αρm )

and the exponent m is chosen in the adaptation process. In the case of a Gaussian blurring function (see Figure 2), the P-deblurring function is given by

P(ρ)=exp[−αρm+(ρ2⁄2σ2)]

where σ is the standard deviation of the Gaussian function. Hence, the problem of choosing H(ρ) becomes the problem of choosing appropriate values of α, m, and σ in the adaptation process.

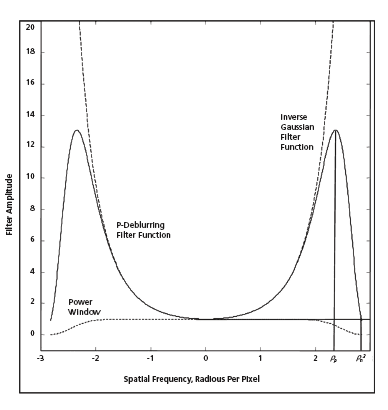
A complete characterization of the effect of the power window and a complete description of the adaptation process would greatly exceed the space available for this article. It must suffice to summarize as follows: The power window preserves most of the spatial-frequency components in its pass band while its attenuation increases rapidly but smoothly with increasing spatial frequency in a transition band, which lies between a peak at the outer edge (ρp)of the pass band and a transition point (ρn) defined as the spatial frequency above which the noise signal exceeds the input image signal. The smoothness of the transition helps to limit a ripple effect that can be especially pronounced in the outputs of prior, more-abrupt-edged deblurring filters. In the deblurring process, the energies of the signal and noise components of the image are estimated in order to estimate the pass band and transition band of the filter and, thereby, to provide guidance for choosing the parameters α, m, and σ. The main criteria applied in selecting the parameters are expressed by the following equations:

P(ρ)>1 for ρ<ρn

P(ρ)=1 for ρ=ρn

P(ρ)<1 for ρ>ρn

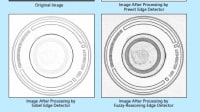
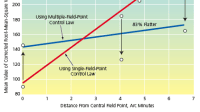
The adaptively designed deblurring filter is able to deblur the image by a desired amount based on the estimated or known blurring function, while reducing noise in the output image. The effectiveness of the adaptive deblurring algorithm has been demonstrated in human-perception experiments involving comparisons of blurred noisy images with their P-deblurred counterparts.

This work was done by S. Susan Young, Ronald G. Driggers, Brian P. Teaney, and Eddie L. Jacobs of the Army Research Laboratory.

ARL-0027

Topics:
Filters Imaging and visualization Mathematical models Optics Physical Sciences Research and development Simulation and modeling
This Brief includes a Technical Support Package (TSP).
Document cover
Adaptive Deblurring of Noisy Images

(reference ARL-0027) is currently available for download from the TSP library.

Don't have an account?

More From SAE Media Group

    Magazine cover
    Defense Tech Briefs Magazine

    This article first appeared in the April, 2008 issue of Defense Tech Briefs Magazine (Vol. 2 No. 2).

    Read more articles from the archives here.

    Overview

    The document titled "Adaptive Deblurring of Noisy Images," authored by S. Susan Young, Ronald G. Driggers, Brian P. Teaney, and Eddie L. Jacobs, presents a comprehensive study on techniques for enhancing image quality by addressing issues of blurriness and noise. Published by the U.S. Army Research Laboratory in October 2007, the report spans the period from June 2006 to September 2007 and is designated as ARL-TR-4276.

    The introduction outlines the significance of image deblurring in various applications, particularly in military and surveillance contexts, where clarity of visual information is crucial. The report delves into the design and properties of a P-Deblurring Filter, which is central to the proposed methods. Key properties of this filter include the Peak Point, Noise Separation Frequency Point, and Cutoff Frequency Point, which are essential for effectively distinguishing between signal and noise in images.

    The document details two primary design approaches for the P-Deblurring Filter: Direct Design and Adaptive Design. The Direct Design method focuses on creating a filter based on predetermined parameters, while the Adaptive Design method involves estimating noise energy and dynamically adjusting the filter parameters to optimize performance based on the specific characteristics of the input image.

    A significant portion of the report is dedicated to the Perception Experiment, which evaluates the effectiveness of the proposed deblurring techniques through subjective assessments of image quality. The results of these experiments are analyzed in detail, providing insights into the performance of the P-Deblurring Filter in various scenarios.

    The conclusions drawn from the study emphasize the potential of adaptive filtering techniques to significantly improve the clarity of noisy images. The findings suggest that the proposed methods can be effectively applied in real-world situations, enhancing the usability of images in critical applications.

    Overall, the report contributes valuable knowledge to the field of image processing, particularly in the context of military and surveillance operations, where the ability to extract clear information from noisy images can have substantial implications. The document is approved for public release, ensuring that the findings can be disseminated for broader use and application.

    Top Stories

    INSIDERDefense

    Feature Image F-35 Proves Nuke Drop Performance in Stockpile Flight Testing

    INSIDERMaterials

    Feature Image Using Ultrabright X-Rays to Test Materials for Ultrafast Aircraft

    INSIDERManufacturing & Prototyping

    Feature Image Stevens Researchers Test Morkovin's Hypothesis for Major Hypersonic Flight...

    INSIDERManufacturing & Prototyping

    Feature Image New 3D-Printable Nanocomposite Prevents Overheating in Military Electronics

    INSIDERRF & Microwave Electronics

    Feature Image L3Harris Starts Low Rate Production Of New F-16 Viper Shield

    INSIDERRF & Microwave Electronics

    Feature Image F-22 Pilot Controls Drone With Tablet

    Webcasts