MOBILITY ENGINEERING Produced by SAE Media Group
MOBILITY ENGINEERING
Magazines
Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Study of Membrane Optics for Lightweight Space Telescopes

Unimorph piezoelectric actuators would be used to control shapes of membrane mirrors.

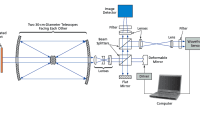
Astudy has been performed to establish a foundation for the analysis, design, and further development of inplane- actuated deformable membrane mirrors for lightweight spaceborne telescopes. It is envisioned that the telescopes, having typical mirror diameters of 20 m or larger, would be stowed compactly for launch and transport, then deployed in orbit around the Earth for use in surveillance of the Earth and in exploration of deep space.

Of Three Types of In-Plane Actuators that could be used on deformable mirrors, the unimorph type was considered for membrane optics in the study reported here. In each case, the arrows depict expansion or contraction in the piezoelectric layer.
With respect to a given mirror membrane, "in-plane-actuated" as used here signifies that actuators would be bonded to the membrane, where they would, variously, expand or contract along the membrane surface upon application of suitable voltages and would thereby locally impart bending moments to deform the mirror surface (see figure). The actuator voltages would be chosen so that the deformations would form the mirror into an acceptably close approximation of a precise shape needed for optical control. For the purpose of this study, it was assumed that actuators for outerspace membrane optics would be, more specifically, unimorph piezoelectric actuators, each bonded to one surface of the membrane (usually, opposite the mirror surface).

In the study, the underlying differential equations for a unimorph-actuated membrane were developed, using a plate-membrane model to represent the elastic behavior of the membrane, along with applicable assumptions of quasi-static piezoelectric theory and a piezoelectric-thermal analogy. A finite-element model corresponding to the differential equations was developed and used to generate theoretical predictions for a 0.127-m diameter deformable mirror testbed. A boundary tension field needed for the finite-element model was determined by use of laservibrometer data. A nonlinear solution technique was used to incorporate the stiffening of the membrane by applied tension. Deformation data calculated by use of influence functions derived from the finite-element model for the static case were compared with experimental deformation data, then a least-squares approach was followed in creating an influencefunction matrix, which, in turn, was incorporated into a quasi-static control algorithm. In a subsequent test of the algorithm, simultaneous tracking of the Zernike tip, tilt, and defocus modes was demonstrated. (Zernike modes are so named because they are characterized by orthonormal polynomials, developed by Frits Zernike, that arise in the mathematical treatment of wavefronts in optical systems having circular pupils.)

Analytical solutions to plate-membrane and beam-string ordinary differential equations representing the deformable-mirror equations were developed. A simplified approach to modeling in axisymmetric cases also was developed. Significantly, it was shown both analytically and through numerical analysis that the result of static actuation for a mirror with a discrete electrode pattern and a high tension- to-stiffness ratio is simply a localized piston displacement (a displacement perpendicular to the surface of the membrane) in the region of the actuator.

Next, a static control strategy denoted the modal transformation method was developed. The method was implemented in a finite-element simulation to demonstrate the capability to form Zernike surfaces within a clear aperture region by use of a number of statically actuated structural modes.

The problem of scaling for membrane optics was addressed. Linear mathematical models were shown to correctly represent the behaviors of small-scale laboratory models, but fully nonlinear models were found to be necessary for describing the behaviors of larger-aperture membrane mirrors. The results of this part of the study have been interpreted to suggest that nonlinear effects must be considered in feasibility studies for future largeaperture membrane mirrors for telescopes.

This work was done by Michael J. Shepard of the Air Force Institute of Technology for the Air Force Research Laboratory. For more information, download the Technical Support Package (free white paper) at www.defensetechbriefs.com/tsp  under the Photonics category. AFRL-0005

Topics:
Exteriors Mathematical models Mirrors Mirrors Optics Photonics Sensors and actuators Simulation and modeling
This Brief includes a Technical Support Package (TSP).
Document cover
Study of Membrane Optics for Lightweight Space

(reference AFRL-0005) is currently available for download from the TSP library.

Don't have an account?

More From SAE Media Group

    Magazine cover
    Defense Tech Briefs Magazine

    This article first appeared in the August, 2007 issue of Defense Tech Briefs Magazine (Vol. 1 No. 4).

    Read more articles from the archives here.

    Overview

    The document is a dissertation by Michael J. Shepherd that focuses on the development of lightweight, in-plane actuated deformable mirrors for space telescopes. The research aims to improve deep space exploration and Earth surveillance by creating large diameter light-gathering apertures that can be compactly stowed and deployed in orbit.

    The document is organized into eight chapters, beginning with an introduction to the research area and the thesis statement. It provides contextual background on membrane optics, outlining current research in the field. The development of piezoelectric theory is discussed, including the piezoelectric-thermal analogy and the governing equations for in-plane actuated circular plate-membranes.

    Chapter IV presents non-linear finite element modeling and experimental closed-loop quasi-static control efforts conducted on a 0.127m diameter test article, specifically the AFIT deformable mirror testbed. This chapter highlights the practical applications of the theoretical concepts introduced earlier.

    In Chapter V, the analysis of a linear piecewise continuous axisymmetric ordinary differential equation for in-plane actuated beam-strings and plate-membranes is provided. The chapter presents both analytical and approximation methods, comparing results with the non-linear finite element model from Chapter IV.

    Chapter VI introduces the Modal Transformation Method, which utilizes a combination of Bessel-based statically actuated vibration mode shapes for static surface control. This method addresses the incompatibility of the Zernike basis set with the fixed edge condition of the deformable mirror.

    Chapter VII discusses the implications of scale in membrane optics, demonstrating through finite element simulation that the model's scale significantly affects surface deformation's shape and magnitude. This chapter emphasizes the importance of considering scale in the design and testing of optical systems.

    The document concludes with an appendix, bibliography, and index, providing additional resources and references for further exploration of the topics discussed. Overall, Shepherd's research contributes valuable insights into the design and control of deformable mirrors, which are crucial for advancing optical systems in space applications. The findings have the potential to enhance the performance of space telescopes, enabling more effective exploration and observation of celestial bodies.

    Top Stories

    INSIDERManufacturing & Prototyping

    Feature Image NASA’s Quiet Supersonic Demonstrator Jet Completes First Flight

    INSIDERDefense

    Feature Image AUSA 2025: The Army's New Anti-Vehicle Terrain Shaping Munition is Ready for...

    INSIDERManufacturing & Prototyping

    Feature Image AUSA 2025: Secretary Driscoll Wants Army to Save Time and Money by 3D-Printing...

    INSIDERDesign

    Feature Image Helsing Unveils New Autonomous Fighter Jet 'CA-1 Europa'

    PodcastsManned Systems

    Feature Image Autonomous Targeting Systems for a New Autonomous Ground Vehicle

    INSIDERAerospace

    Feature Image AUSA 2025: New CMOSS Chassis, Plug-in-Card Prototypes in Development for Army...

    Webcasts