MOBILITY ENGINEERING Produced by SAE Media Group
MOBILITY ENGINEERING
Magazines
Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Using Fisher Information Criteria for Chemical Sensor Selection via Convex Optimization Methods

Technique developed for simple linear sensor systems can be applied to broader array scenarios.

The design of chemical sensor arrays from the standpoint of chemical sensor selection and error quantification has historically proceeded as an ad hoc process. Frequently, chemical sensors are developed not as general purpose sensing devices, but as analyte or chemical class specific detectors. When such single purpose devices are integrated together as a chemical sensor array, it is unclear a priori how well they will function in concert with each other to provide expanded capabilities, an observation that is true of the integration of analytical instruments as well.

Further complicating the combination and optimization of these devices is that it is semantically unclear precisely what the combined device or array ought to do. Defining what a combined sensing device ought to do is difficult and highly dependent upon the analytical task the array will be intended to support, as well as the specific goals of the array designer.

In the face of an otherwise unspecified sensing task, it is reasonable to assume that the practitioner should attempt to minimize the global error of the array, or conversely, to maximize the signal. The question remains, however, as to how to best fulfill this objective. While a hypothetical practitioner may be able to take an exhaustive approach to sensor array design by experimentally evaluating all possible sensor combinations, this method quickly becomes infeasible as the number of sensors relative to array slots becomes coequal or large. In the rare cases when a sensor array optimization has been attempted (as opposed to using whatever sensors were immediately available), it is this aforementioned approach of combinatorial experimentation which historically has typified chemical sensor array design, and thus, severely limited the optimization of sensor arrays. Alternative approaches to array design based on neural networks and machine learning have also been tried. However, due to their opacity, these methods fail to provide significant insight into the chemical detection problem or to suggest subsequent ways to further improve the array design. Consequently, an explicit, precise, and mathematically rigorous approach to chemical sensor array design and optimization is greatly desired.

Given its wide range of applications, it is surprising that the literature centered on chemical sensor array optimization strategies is rather sparse, despite the relative frequency of reports describing specific sensor arrays and applications. A notable exception is the Fisher information matrix-based approach proposed by Pearce and Sánchez-Montaes and theoretically applied to simple linear sensor systems with uncorrelated noise. Unfortunately, this methodology has not been greatly developed, most likely due to the mathematical complexities and difficulties presented by implementing this program, as well as the accompanying change in mentality this forces upon the typical practitioner in the chemical sensing field.

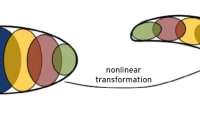
This research further develops the use of the Fisher information matrix as a quantitative descriptor for hypothetical chemical sensor array scenarios in which a collection of co-located sensors respond to chemical mixtures resulting from a pool of possible analytes. It assumes that the underlying sensors provide additive linear responses with respect to the system of analytes and that they may exhibit statistically correlated noise. The latter is important as correlated measurement error is realistic, yet frequently unacknowledged in the literature. The former is generally a reasonable assumption in low concentration regimes, which typify the bulk of analytical sensing applications, and present the greatest challenges regarding desired sensitivity and selectivity. This work describes how the positive (semi)definite nature of the Fisher information matrix enables algorithmic chemical sensor array design via convex optimization techniques.

This work was done by Adam C. Knapp and Kevin J. Johnson of the Navy Technology Center for Safety and Survivability, Chemistry Division, for the Naval Research Laboratory. NRL-0070

Topics:
Aerospace Artificial intelligence (AI) Chemicals Data acquisition and handling Machine learning Neural networks Sensors Sensors and actuators
This Brief includes a Technical Support Package (TSP).
Document cover
Using Fisher Information Criteria for Chemical Sensor Selection via Convex Optimization Methods

(reference NRL-0070) is currently available for download from the TSP library.

Don't have an account?

More From SAE Media Group

    Magazine cover
    Aerospace & Defense Technology Magazine

    This article first appeared in the April, 2017 issue of Aerospace & Defense Technology Magazine (Vol. 2 No. 2).

    Read more articles from this issue here.

    Read more articles from the archives here.

    Overview

    The document titled "Using Fisher Information Criteria for Chemical Sensor Selection via Convex Optimization Methods" presents a methodology for the optimal selection of chemical sensors within a sensing array. Authored by Adam C. Knapp and Kevin J. Johnson from the Naval Research Laboratory, the report emphasizes the importance of maximizing signal strength or minimizing global error in sensor selection, which is task-specific.

    The core of the methodology is based on the Fisher information matrix, a statistical tool that quantifies the amount of information that an observable random variable carries about an unknown parameter. The report details how the determinant of the inverse Fisher information matrix can be used to assess global error volume, thereby guiding the selection of the most effective sensors. By employing a suitable probabilistic noise model for the chemical sensing array and the available sensors, practitioners can parameterize the Fisher information matrix to identify the best sensor configurations through an optimization process.

    The document outlines the positive definite nature of the Fisher information matrix, which allows for the application of convex optimization techniques. This approach is particularly beneficial as it ensures that the optimization problem can be solved efficiently, leading to near-optimal sensor selection. The report includes derivations of the necessary setup, expressions, and constraints required for implementing this optimization procedure.

    Additionally, the report discusses the general applicability of Fisher information in sensor systems, the relationship between Fisher information and the Cramér-Rao inequality, and provides a lower bound derivation for the Fisher information matrix. It also covers the background on convex optimization, the use of elliptically contoured distributions as a correlated noise model for chemical sensor arrays, and the necessary gradients and Hessians for the Fisher information matrices.

    In conclusion, this report serves as a comprehensive guide for researchers and practitioners in the field of chemical sensing, offering a robust framework for sensor selection that leverages statistical principles and optimization methods. The findings aim to enhance the effectiveness of chemical sensing applications, ultimately contributing to improved safety and operational capabilities in various environments.

    Top Stories

    INSIDERDefense

    Feature Image F-35 Proves Nuke Drop Performance in Stockpile Flight Testing

    INSIDERMaterials

    Feature Image Using Ultrabright X-Rays to Test Materials for Ultrafast Aircraft

    INSIDERManufacturing & Prototyping

    Feature Image Stevens Researchers Test Morkovin's Hypothesis for Major Hypersonic Flight...

    INSIDERManufacturing & Prototyping

    Feature Image New 3D-Printable Nanocomposite Prevents Overheating in Military Electronics

    INSIDERRF & Microwave Electronics

    Feature Image L3Harris Starts Low Rate Production Of New F-16 Viper Shield

    INSIDERRF & Microwave Electronics

    Feature Image F-22 Pilot Controls Drone With Tablet

    Webcasts