Creating and Verifying Stable AI-Controlled Systems in a Rigorous, Flexible Way
Neural network controllers provide complex robots with stability guarantees, paving the way for the safer deployment of autonomous vehicles and industrial machines.

Neural networks have made a seismic impact on how engineers design controllers for robots, catalyzing more adaptive and efficient machines. Still, these brain-like machine-learning systems are a double-edged sword: Their complexity makes them powerful, but it also makes it difficult to guarantee that a robot powered by a neural network will safely accomplish its task.
The traditional way to verify safety and stability is through techniques called Lyapunov functions. If you can find a Lyapunov function whose value consistently decreases, then you can know that unsafe or unstable situations associated with higher values will never happen. For robots controlled by neural networks, though, prior approaches for verifying Lyapunov conditions didn’t scale well to complex machines.
Researchers from MIT’s Computer Science and Artificial Intelligence Laboratory (CSAIL) and elsewhere have now developed new techniques that rigorously certify Lyapunov calculations in more elaborate systems. Their algorithm efficiently searches for and verifies a Lyapunov function, providing a stability guarantee for the system. This approach could potentially enable safer deployment of robots and autonomous vehicles, including aircraft and spacecraft.
To outperform previous algorithms, the researchers found a frugal shortcut to the training and verification process. They generated cheaper counterexamples — for example, adversarial data from sensors that could’ve thrown off the controller — and then optimized the robotic system to account for them. Understanding these edge cases helped machines learn how to handle challenging circumstances, which enabled them to operate safely in a wider range of conditions than previously possible. Then, they developed a novel verification formulation that enables the use of a scalable neural network verifier, α,β-CROWN, to provide rigorous worst-case scenario guarantees beyond the counterexamples.
“We’ve seen some impressive empirical performances in AI-controlled machines like humanoids and robotic dogs, but these AI controllers lack the formal guarantees that are crucial for safety-critical systems,” says Lujie Yang, MIT Electrical Engineering and Computer Science (EECS) Ph.D. student and CSAIL affiliate who is a co-lead author of a new paper on the project alongside Toyota Research Institute researcher Hongkai Dai SM ’12, PhD ’16. “Our work bridges the gap between that level of performance from neural network controllers and the safety guarantees needed to deploy more complex neural network controllers in the real world,” notes Yang.
For a digital demonstration, the team simulated how a quadrotor drone with lidar sensors would stabilize in a two-dimensional environment. Their algorithm successfully guided the drone to a stable hover position, using only the limited environmental information provided by the lidar sensors. In two other experiments, their approach enabled the stable operation of two simulated robotic systems over a wider range of conditions: an inverted pendulum and a path-tracking vehicle. These experiments, though modest, are relatively more complex than what the neural network verification community could have done before, especially because they included sensor models.
“Unlike common machine learning problems, the rigorous use of neural networks as Lyapunov functions requires solving hard global optimization problems, and thus scalability is the key bottleneck,” says Sicun Gao, Associate Professor of Computer Science and Engineering at the University of California at San Diego, who wasn’t involved in this work. “The current work makes an important contribution by developing algorithmic approaches that are much better tailored to the particular use of neural networks as Lyapunov functions in control problems. It achieves impressive improvement in scalability and the quality of solutions over existing approaches. The work opens up exciting directions for further development of optimization algorithms for neural Lyapunov methods and the rigorous use of deep learning in control and robotics in general.”
Yang and her colleagues’ stability approach has potential wide-ranging applications where guaranteeing safety is crucial. It could help ensure a smoother ride for autonomous vehicles, like aircraft and spacecraft. Likewise, a drone delivering items or mapping out different terrains could benefit from such safety guarantees.
The techniques developed here are very general and aren’t just specific to robotics; the same techniques could potentially assist with other applications, such as biomedicine and industrial processing, in the future.
While the technique is an upgrade from prior works in terms of scalability, the researchers are exploring how it can perform better in systems with higher dimensions. They’d also like to account for data beyond lidar readings, like images and point clouds.
As a future research direction, the team would like to provide the same stability guarantees for systems that are in uncertain environments and subject to disturbances. For instance, if a drone faces a strong gust of wind, Yang and her colleagues want to ensure it’ll still fly steadily and complete the desired task.
This work was performed by a team of researchers from MIT’s Computer Science and Artificial Intelligence Laboratory. For more information, download the Technical Support Package (free white paper) below. ADTTSP-09244
This Brief includes a Technical Support Package (TSP).
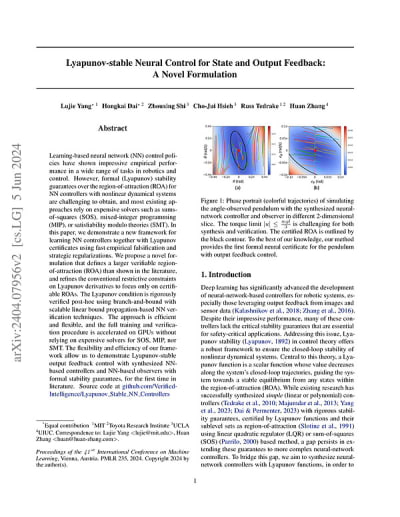
Lyapunov-stable Neural Control for State and Output Feedback: A Novel Formulation
(reference ADTTSP-09244) is currently available for download from the TSP library.
Don't have an account?
Top Stories
NewsRF & Microwave Electronics
![]() Microvision Aquires Luminar, Plans Relationship Restoration, Multi-industry Push
Microvision Aquires Luminar, Plans Relationship Restoration, Multi-industry Push
INSIDERAerospace
![]() A Next Generation Helmet System for Navy Pilots
A Next Generation Helmet System for Navy Pilots
INSIDERDesign
![]() New Raytheon and Lockheed Martin Agreements Expand Missile Defense Production
New Raytheon and Lockheed Martin Agreements Expand Missile Defense Production
INSIDERMaterials
![]() How Airbus is Using w-DED to 3D Print Larger Titanium Airplane Parts
How Airbus is Using w-DED to 3D Print Larger Titanium Airplane Parts
NewsPower
![]() Ford Announces 48-Volt Architecture for Future Electric Truck
Ford Announces 48-Volt Architecture for Future Electric Truck
ArticlesAR/AI
Webcasts
Electronics & Computers
![]() Cooling a New Generation of Aerospace and Defense Embedded...
Cooling a New Generation of Aerospace and Defense Embedded...
Automotive
![]() Battery Abuse Testing: Pushing to Failure
Battery Abuse Testing: Pushing to Failure
Power
![]() A FREE Two-Day Event Dedicated to Connected Mobility
A FREE Two-Day Event Dedicated to Connected Mobility
Unmanned Systems
![]() Quiet, Please: NVH Improvement Opportunities in the Early Design Cycle
Quiet, Please: NVH Improvement Opportunities in the Early Design Cycle
Automotive
![]() Advantages of Smart Power Distribution Unit Design for Automotive &...
Advantages of Smart Power Distribution Unit Design for Automotive &...
Energy
![]() Sesame Solar's Nanogrid Tech Promises Major Gains in Drone Endurance
Sesame Solar's Nanogrid Tech Promises Major Gains in Drone Endurance


































