An Integrated Framework for Complex Radar System Design
Modern radar systems are complex and depend heavily on advanced signal processing algorithms to improve their detection performance. At the same time, the radio front-end must meet challenging specifications with a combination of available components, implementation technologies, regulatory constraints, requirements from the system, and signal processing. This application example shows how NI's Visual System Simulator™ (VSS) system simulation software enables radar system architects and RF component manufacturers to design, validate, and prototype a radar system.

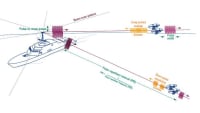
The project in this example, Pulse_Doppler_Radar_System.emp, illustrates key models and simulation capabilities available for practical radar design. The project and resulting measurements highlight how to configure a pulse-Doppler (PD) radar and set up the simulation to obtain the metrics of interest for radar development. The entire PD radar system project includes a linear FM (LFM) chirp signal generator, RF transmitter, antennas, clutter, RF receiver, moving target detector (MTD), constant false alarm rate (CFAR) processor, and signal detector for simulation purposes.
Theory of Operation
PD radars produce velocity data by reflecting a microwave signal from a given target and analyzing how the frequency of the returned signal has shifted due to the object's motion. This variation in frequency provides the radial component of a target's velocity relative to the radar. The radar determines the frequency shift by measuring the phase change that occurs in the electromagnetic (EM) pulse over a series of pulses. By measuring the Doppler rate, the radar is able to determine the relative velocity of all objects returning echoes to the radar system, including planes, vehicles, and ground features.
As the reflector (target) moves between each transmit pulse, the returned signal has a phase difference or phase shift from pulse to pulse. This causes the reflector to produce Doppler modulation on the reflected signal. For example, assume a target at a distance R has a radial velocity component of Vr. The round-trip distance to target is 2R. This is equivalent to 2R/ wavelengths or (2R )2/ 4=R /radians.
If the phase of the transmitted signal is φ0, then the phase of the received signal will be:
φ = φ0 + 4πR/λ
The change in phase between pulses is:
dφ/dt = (4π/λ)*(dR/dt) = (4π/λ)*Vr
System Setup

The main radar system diagram in Figure 1 includes the following building blocks: linear chirp source, RF transmitter and receiver, and target and propagation models, as well as receiver baseband signal processing blocks, including moving target indicator (MTI), MTD, and CFAR. User-defined parameters specifying the gain, bandwidth, and carrier frequency of both the transmitter and receiver sub-blocks can be set to values based on test specifications. A detailed look at the individual components explains how this PD radar works.

The linear chirp source (first block to the far left of the system diagram) generates a linear FM chirp signal, also known as a PD signal. The linear chirp pulse source consists of basic parameters that can be configured according to user specifications, such as pulse repetition frequency (PRF), pulse duty cycle, start/stop frequency, and sampling frequency. The pulse repetition interval (PRI) denotes the time difference between the starts of two consecutive pulses, shown in Figure 2. The chirp duration (pulse on) is a function of duty cycle and PRI and is calculated as the product of the two; the duty cycle is a percentage and can take any non-negative value up to and including 100 percent.
During the active portion of the chirp, this block outputs a signal with instantaneous frequency that changes linearly between the start and stop frequency parameters. These two parameters can have any valid frequency value, resulting in signals that can have either increasing or decreasing frequencies at the start of the chirp. Designers are also able to specify the ratio of rise and pulse on. This parameter is a percentage and can have any non-negative value up to and including 100 percent.
The signal power during the active portion of the chirp is set by the peak power parameter of the linear chirp signal generator. A non-zero initial delay may be defined for the chirp pulse; this delay may take on any non-negative value and a warning is generated if this delay is greater than the PRI. The center frequency of the chirp signal may be user defined. If left empty, it is set to the average of the start and stop frequencies. Similarly, the sampling frequency may also be user defined; if left empty, it is calculated based on the global variable “_SMPFRQ”. In this example, the chirp signal level is set to 0 dBm, PRF = 2 kHz and DUTY = 25 percent.
The next block in the chain, a coupled correlator block, is commonly used for pulse compression in radar receivers. Pulse compression is a signal processing technique used to increase the range resolution, as well as the signal-to-noise ratio (SNR), by modulating the transmitted pulse and then correlating the received signal with the transmitted pulse. In this example, a block performs a correlation between the signal reflected from a radar target and the transmitted signal. This requires the coupled correlator to buffer enough samples to accommodate a full PRI before it can process the chirp. To ensure a successful simulation of such scenarios, the sampling frequency should be carefully selected. The minimum value for the sampling frequency parameter would be the bandwidth of the radar signal (FSTART-FSTOP). If spectral measurements are desired, the sampling frequency can be set to a larger value.

The signal next passes through the RF transmitter responsible for frequency up-conversion, filtering, and signal amplification before being radiated through the antenna toward the target. Both the RF transmitter and receiver subcircuits define the single stage upconverter and downconverter that are each composed of an oscillator, mixer, amplifier, and filter, as shown in Figure 3. Users may replace these subcircuits with their own particular implementations. To fully model the entire system, this example includes a subcircuit that models the propagation channel between TX/RX antennas, as well as the radar target. With this particular setup, users may specify the distance and relative velocity of the target, their RCS and RCS fluctuations, and also model jammers and clutter that are often present in radar systems.
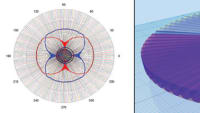
The Doppler frequency offset, target distance, and angles of arrival (THETA/PHI) are defined in a data file and vary over time. These parameters are used to define the target model. The clutter magnitude distribution is set to Rayleigh and the clutter power spectrum is formed as Weibull. The antenna radiation patterns (Figure 4) for both the transmit and receive antennas are based on file-based data from a separate EM simulation, but could also be similarly modeled with measured data. The receiver filters the incoming reflected signal prior to amplification via a low-noise amplifier (LNA), which is then down-converted through a mixer and further filtered before input into the coupled correlator. The correlator performs correlation of the downconverted reflected signal with a coupled signal representing the input to the RF transmitter.

Radar searching, tracking, and other operations are usually carried out over a specified range (receive) window and defined by the difference between the radar maximum and minimum range. Reflected signals from all targets within the receive window are collected and passed through a matched filter circuitry to perform pulse compression. The correlation processor is often performed digitally using the fast Fourier transform (FFT).
To detect the moving object more effectively, MTD, which is based on a high-performance signal processing algorithm for PD radar, is used. A bank of Doppler filters or FFT operators cover all possible expected target Doppler shifts. The output of the MTD is used for the CFAR processing. Measurements for the detection and false alarm rate are provided. The MTI is used to remove stationary objects, the MTD is used to identify the remaining moving target with the FFT size set to 64, and the CFAR performs a sliding average to ensure that the detected signal is greater than a set threshold.
Simulation Results

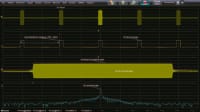
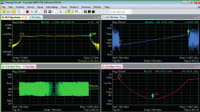
Under these settings, the simulation results are displayed in Figure 5. The radar signal waveform is measured in the time domain at the receiver input. Because the target return signal is often blocked by clutter, jamming, and noise, detection in the time domain is not possible and an MTD is used to perform the Doppler and range detection in the frequency domain. In the MTD model, the data are grouped for corresponding target range and Doppler frequency. Afterwards, a CFAR processor is used to set the decision threshold based on the required probabilities of detection and false alarm.
Chirp waveform: The time-domain graph shows the transmitted pulse, received pulse, and the pulse after the transmit/receive correlation. The correlator output is used in the baseband-received signal processing blocks to turn it into useful target information.
Antenna pattern: The radial plot shows the combined transmit and receive antenna pattern. When the simulation is run for the first time, the antenna parameters PHI and THETA are swept to obtain this data (see also antenna pattern VSS diagram for the swept variable setting).
MTI output: The time-domain plot shows the output of the MTI, which uses a second-order delay line canceler to remove effects of stationary clutter and leave Doppler information in the signal.
The graph shows the system metrics, including the detected speed, Doppler, probability of detection (PoD), radar cross section (RCS), and distance across multiple pulses.
Conclusion
This application example illustrates how key models and simulation capabilities within VSS enable practical radar design. Since much of the simulation control setup and radar system details (operating conditions) have been parameterized, this project can be used as a template for different PD applications. The radar signal is a function of PRF, power, and pulse width (duty cycle) and these parameters can be modified for different cases. In the simulation, the radar signal also can be replaced by any defined signal through the data file reader in which the recorded or other custom data source can be easily used.
This article was written by David Vye, Technical Marketing Director, National Instruments (Austin, TX). For more information, visit here .
Top Stories
INSIDERManufacturing & Prototyping
![]() How Airbus is Using w-DED to 3D Print Larger Titanium Airplane Parts
How Airbus is Using w-DED to 3D Print Larger Titanium Airplane Parts
INSIDERManned Systems
![]() FAA to Replace Aging Network of Ground-Based Radars
FAA to Replace Aging Network of Ground-Based Radars
NewsTransportation
![]() CES 2026: Bosch is Ready to Bring AI to Your (Likely ICE-powered) Vehicle
CES 2026: Bosch is Ready to Bring AI to Your (Likely ICE-powered) Vehicle
NewsSoftware
![]() Accelerating Down the Road to Autonomy
Accelerating Down the Road to Autonomy
EditorialDesign
![]() DarkSky One Wants to Make the World a Darker Place
DarkSky One Wants to Make the World a Darker Place
INSIDERMaterials
![]() Can This Self-Healing Composite Make Airplane and Spacecraft Components Last...
Can This Self-Healing Composite Make Airplane and Spacecraft Components Last...
Webcasts
Defense
![]() How Sift's Unified Observability Platform Accelerates Drone Innovation
How Sift's Unified Observability Platform Accelerates Drone Innovation
Automotive
![]() E/E Architecture Redefined: Building Smarter, Safer, and Scalable...
E/E Architecture Redefined: Building Smarter, Safer, and Scalable...
Power
![]() Hydrogen Engines Are Heating Up for Heavy Duty
Hydrogen Engines Are Heating Up for Heavy Duty
Electronics & Computers
![]() Advantages of Smart Power Distribution Unit Design for Automotive...
Advantages of Smart Power Distribution Unit Design for Automotive...
Unmanned Systems
![]() Quiet, Please: NVH Improvement Opportunities in the Early Design...
Quiet, Please: NVH Improvement Opportunities in the Early Design...