MOBILITY ENGINEERING Produced by SAE Media Group
MOBILITY ENGINEERING
Magazines
Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Magazine cover

Current Issue

Archives

Optical-Fiber Infrasound Sensors

Features include directionality and relatively flat frequency response.

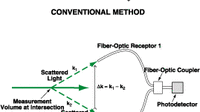
Optical-fiber infrasound sensors (OFISs) are being developed for detecting acoustic pressures in the frequency range from a few millihertz to a few hertz. As explained below, these sensors were conceived to overcome some of the limitations of prior infrasound sensors based on pipe filters connected to microbarographs.

Figure 1. An OFIS includes a fiber-optic Mach-Zehnder interferometer that measures acoustic strain in a sealed hose. The length and diameter of the hose are not critical and can be chosen according to considerations of sensitivity, directionality, and suppression of noise. In one prototype OFIS, the hose is 2.5 cm in diameter and 89 m long.
An OFIS includes a sealed hose and a fiber-optic Mach-Zehnder interferometer that is sensitive to acoustically induced fluctuations in strain in the hose. The OFIS (see Figure 1) includes two optical fibers wrapped around and along the hose in slight tension in two spiral patterns having equal pitch. Both fibers are doubled back on themselves, but with different spacings, so that the two fibers undergo different amounts of strain when the hose expands or contracts in response to changing air pressure. Light from a laser is coupled into both fibers via a fiber-optic splitter and a piezoelectric modulator, which is excited at a suitable frequency. After traveling along the optical fibers, the laser beams are coupled out via another fiber-optic splitter and fed to a photodetector, wherein the beams interfere. The output of the photodetector is demodulated by a lock-in amplifier synchronized with the modulator excitation. The output of the lock-in amplifier consists of two interference signals in quadrature. These signals are sampled at a suitable rate (e.g., 200 Hz) and the samples are processed to obtain the strain-fluctuation signal and, hence, the desired acoustic-pressure signal.

The principal source of acoustic noise in the infrasound frequency range is wind turbulence. In a typical prior infrasound sensor based on a pipe filter connected to a microbarograph, the sound is summed acoustically from multiple locations connected to the microbarograph via the pipe filter in order to obtain an averaging or smoothing effect that suppresses the relative contribution of noise. Unfortunately, the acoustic sum is not a true average and is affected by the frequency response of the pipe filter, which response is not flat across the entire infrasound frequency band and can be determined only with extreme difficulty. In contrast, the response of an OFIS depends on the optical response of the fiber but is substantially independent of the acoustic frequency.

Figure 2. The Directionality of an OFIS increases with length, as illustrated by four example polar plots of relative amplitude (represented by radius) versus angle of incidence (¸ represented by azimuthal angle).
Relative to the output of a microbarograph connected via a pipe filter to multiple sampling locations, the response of the OFIS is a much closer approximation to a true spatial average of acoustic pressure because it is proportional to the integral of strain (and, hence, to the integral of acoustic pressure) along the hose. Another advantageous feature of integration of acoustic pressure along the hose is that the response is directional and can be made more so by simply increasing the length: It can be shown that if the hose is N acoustic wavelengths long at a frequency of interest and the direction of incidence of a wave having that frequency is such that the wavefronts lie at an angle θ with respect to the longitudinal axis of the hose, then the relative amplitude of the integratedpressure signal is given by

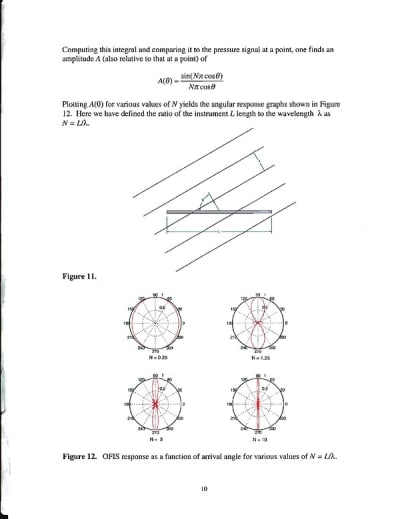
A(θ) = sin[Nπcos(ı)]/Nπcos(θ).

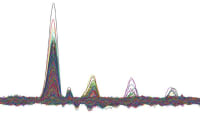
As illustrated by a few examples in Figure 2, this response peaks at broadside incidence (θ = 90°) and becomes more sharply peaked as N increases.

This work was done by Mark A. Zumberge and Jonathan Berger of the University of California for the Defense Threat Reduction Agency. For more information, download the Technical Support Package (free white paper) at www.defensetechbriefs.com/tsp  under the Photonics category. DTRA-0001

Topics:
Acoustics Engine components Engine cooling systems Engines Fiber optics Filters Hoses Photonics Powertrains Pressure
This Brief includes a Technical Support Package (TSP).
Document cover
Optical-Fiber Infrasound Sensors

(reference DTRA-0001) is currently available for download from the TSP library.

Don't have an account?

More From SAE Media Group

    Magazine cover
    Defense Tech Briefs Magazine

    This article first appeared in the August, 2007 issue of Defense Tech Briefs Magazine (Vol. 1 No. 4).

    Read more articles from the archives here.

    Overview

    The document discusses the relationship between integral computations and pressure signals, particularly focusing on the amplitude response of a system as a function of the arrival angle. It introduces a mathematical framework where the amplitude ( A(\theta) ) is expressed in terms of the cosine of the angle ( \theta ) and a parameter ( N ), which is defined as the ratio of the instrument length ( L ) to the wavelength ( \lambda ) (i.e., ( N = \frac{L}{\lambda} )).

    The analysis begins with the computation of an integral that relates to the pressure signal at a specific point. By comparing this integral to the pressure signal, the document derives the expression for amplitude ( A(\theta) ), which is given by:

    [ A(\theta) = N \cdot n \cdot \cos(\theta) ]

    This relationship indicates that the amplitude is influenced by both the parameter ( N ) and the cosine of the angle of arrival, suggesting that the system's response varies with the angle at which the signal arrives.

    The document includes graphical representations (referred to as Figures 11 and 12) that illustrate the angular response of the system for various values of ( N ). These graphs provide visual insights into how the amplitude changes with different angles, highlighting the dependence of the system's response on the ratio of instrument length to wavelength.

    The findings emphasize the importance of understanding the angular response in applications where pressure signals are critical, such as in acoustics or fluid dynamics. By plotting ( A(\theta) ) for different values of ( N ), researchers can better predict how the system will behave under varying conditions, which is essential for designing instruments and interpreting data accurately.

    Overall, the document serves as a concise exploration of the mathematical and graphical analysis of amplitude response in relation to pressure signals, offering valuable insights for researchers and practitioners in fields that rely on such measurements. The interplay between the parameters involved and the resulting angular response is crucial for advancing knowledge in this area.

    Top Stories

    INSIDERDefense

    Feature Image F-35 Proves Nuke Drop Performance in Stockpile Flight Testing

    INSIDERMaterials

    Feature Image Using Ultrabright X-Rays to Test Materials for Ultrafast Aircraft

    INSIDERManufacturing & Prototyping

    Feature Image Stevens Researchers Test Morkovin's Hypothesis for Major Hypersonic Flight...

    INSIDERManufacturing & Prototyping

    Feature Image New 3D-Printable Nanocomposite Prevents Overheating in Military Electronics

    INSIDERRF & Microwave Electronics

    Feature Image L3Harris Starts Low Rate Production Of New F-16 Viper Shield

    INSIDERRF & Microwave Electronics

    Feature Image F-22 Pilot Controls Drone With Tablet

    Webcasts